Plants Do Not Know Mathematics
As per science, the universe was born with the Big Bang. Religions argue that everything was created by an almighty God. Amidst the scientific theories and religious beliefs, our conscious mind wanders aloof in search of truth. Where do we come from? Where are we going? Nobody knows. The only reality in front of us is the Mother Nature. We are infants of the infinite nature, swaddled with love and affection. Nature beckons us to its lap, feeds us, and lullabies us with soothing song. We enjoy nature but seldom think deep about it. Take some relaxed moments and look deeply into the nature. It will reveal the mysteries of Mathematics. Mathematics is everywhere in nature and it is beautiful. Sometimes we will wonder if the creator was a Mathematical genius. He might have manifested his mathematical ideas and spread them in the nature to provide us a spectacular feast. Among the myriads of mathematical wonders, the Fibonacci Numbers and the Golden Ratio have fascinated me the most.
Fibonacci Numbers
Fibonacci numbers consist of a sequence of numbers in which each number is the sum of the two preceding numbers. The order of Fibonacci sequence is as follows:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ………… and so on up to infinity.
If you calculate the ratio of any number to its preceding number, as the sequence increases, you will always get a constant number that will be closer to 1.618; and this number is known as the Golden Ratio, which is a magic number that has enthralled scientists and mathematicians for thousands of years. With its presence in everywhere, Fibonacci numbers are considered as Nature’s Numbering System.
Origin of Fibonacci Numbers
The great Italian Mathematician Leonardo Pisano, who called himself as Fibonacci (meaning “son of Bonacci”), was involved in a deep thought to find the answer to a question: how many pairs of rabbits can be produced from a single pair of rabbits in one year, under some specific conditions? The conditions insist that the female rabbits give birth to pairs consisting one male and female; and rabbits cannot reproduce until they are at least one month old. The fascination of a medieval man with his rabbits resulted in a sequence of numbers, known as Fibonacci Numbers that reveal surprising patterns displayed in the nature. Fibonacci numbers first appeared in his book Liber Abbaci (Book of Abacus) in 1202. It was the reference book of the Western world, from which they learned the fundamentals of Mathematics such as addition, subtraction, multiplication and division.
Fibonacci Numbers in Nature
Fibonacci sequence is displayed everywhere in nature in some naturally occurring patterns, including arrangement of leaves in plants, petals in flowers, branching of tree, scales of pineapple, spirals of sunflower and pine cone, family tree of honeybees and many more.
The arrangement of seeds in the center of a sunflower is in spiral pattern curving left and right. If you count the spirals pointed to the left and right separately, you will get two consecutive Fibonacci numbers. Generally it can be 21 and 34, 34 and 55, or 55 and 89 or the next sequence.
For pine cones the spirals may be either 5 and 8 or 8 and 13. Similarly the number of diagonals of a pineapple will be 8 in one direction and 13 in the other
Have you ever spent some time to count the petals on flowers? It is an interesting fact that the petals of flowers are most often arranged in one of the Fibonacci numbers. For example, Lily and Iris have 3 petals, buttercup and wild rose have 5 petals, delphiniums have 8 petals, corn marigold and ragwort have 13 petals, chicory has 21 petals, and plantain has 34 petals.
In case of the spirals of the sunflower, pineapple and the pine cone the Fibonacci sequence is perfect, whereas the flower petals are the average observations, where the numbers may sometimes be seen doubled due to arrangement of petals in multi-levels.
Family Tree of Honeybees
Honeybees live in their colony called hives. In a colony there is a special female called Queen. There are female Worker bees, produced when Queen is mated with a male, and hence they have two parents. There are male Drone bees produced by Queen’s unfertilized eggs and hence they have only mother but no father.
Now the family tree of a male Drone bee has 1 parent, 2 grandparents, 3 great-great grandparents, 5 great-great-great grandparents and so on. Similarly the female family tree consists of 2 parents, 3 grandparents, 5 great-great grandparents, 8 great-great-great grandparents and so on.They follow the Fibonacci sequence.
Golden Ratio
In the Fibonacci sequence, if we calculate the ratio of each number to its preceding number, and keep on going, we will reach to an interesting number 1.618, which is known as the Golden Ratio. The Golden Ratio is an irrational mathematical constant and is denoted by the Greek letter Phi (ϕ). Its simplest form is a golden rectangle whose length-to-breadth is in the golden ratio 1.618 : 1. This number is seen everywhere in nature, and was used widely in arts, music and architecture.
Golden Ratio has a very special mathematical property. If you add 1 to this number, you will get its square; and if you subtract 1 from this number, you will get its reciprocal.
That is, 1.618+1 = (1.618)2; and 1.618 -1 = (1 ÷ 1.618).
Golden Ratio in Architecture
The famous Greek sculptor Phidias used the Golden Ratio in constructing the sacred temple Parthenon in Greece, dedicated to the Goddess Athena. You can discover Golden Rectangles in the exterior as well as between the columns of this beautiful architecture. The numeric value Phi was given to the Golden Ratio as an honor to this Greek sculptor Phidias.
Egyptians had used Golden Ratio in the construction of Great Pyramid of Giza. Similarly the beauty of golden Ratio can be discovered in ancient and modern architectural wonders including Taj Mahal of India, Notre Dame of Paris, Chartres Cathedral of France, United Nations Building of New York, etc.
Golden Ratio in Art
Great painters had utilized Golden Ratio in their master piece painting works to make them more pleasing and perfect. Leonardo da Vinci used it in his paintings of Mona Lisa and The Vitruvian Man.
Other examples of artwork include: The Sacrament of the Last Supper by Salvador Dali; Holy Family by Michelangelo; Birth of Venus by Botticelli; Crucifixion by Raphael; … and so on.
Golden Ratio in Nature
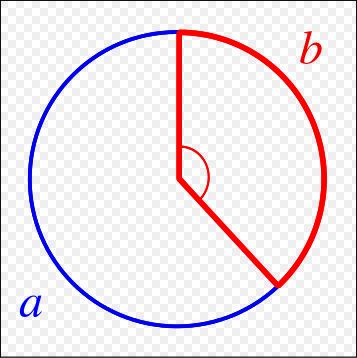
Golden Ratio plays a significant role in the arrangement of leaf on the stem of a plant. Each new leaf grows at an angle offset from that of the leaf below it. Usually the angle between successive leaves is 137.5 degrees. It is known as the Golden Angle. It is the smaller of the two angles formed when dividing the circumference of a circle as per the Golden Ratio. Here the angle subtended by the red arc is the Golden Angle.
Here, (a+b) ÷ a = a ÷ b
Golden Angle = 137.5 degrees = 360 – (360 ÷ ϕ)
It is an arrangement of nature to ensure each leaf gets sunlight without throwing too much shadow on another leaf. It is the natural plan of the plants to arrange maximum number of leaves spiraled around its stem.
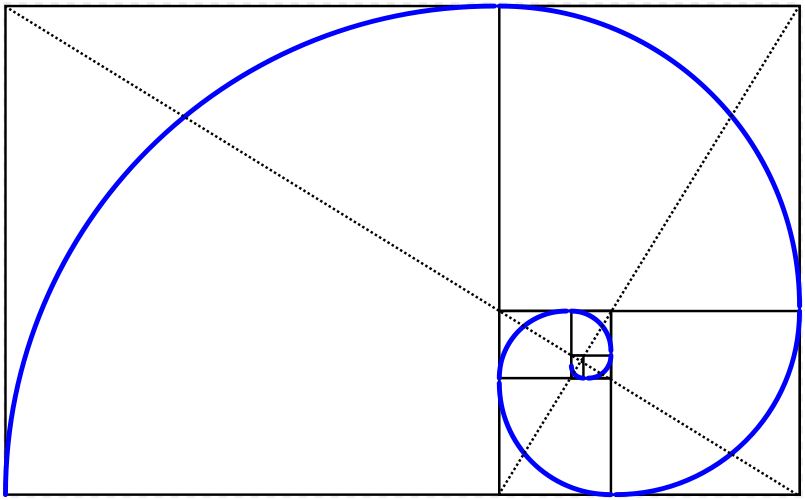
Golden Spiral
Golden spiral is a logarithmic spiral whose growth factor is related to the Golden Ratio. It is based on a series of identically proportioned Golden Rectangles whose length-to-width are in the Golden Ratio 1.618. A Fibonacci spiral, as it increases its size, becomes a Golden spiral, because as the series progresses, the ratios become close to 1.618.
Golden spirals can be seen everywhere in nature, including sunflower, pine cones, human ear, sea shells, hurricane, galaxies, and many more. The beauty of repeating spirals can be seen in the petals of a rose. Succulent plants display the patterns of golden spiral in a perfect manner, with all its leaves getting full access to sunlight, and the roots getting maximum rain, thus providing optimum growth factor.
Aloe polyphylla, commonly known as the Spiral Aloe, seen in the mountain peaks of Kingdom of Lesotho, is famous for its symmetrical five point spiral growth and is a classic example for Fibonacci Spiral.
Golden Ratio in Humans
An ideal human body displays amazing proportions of Golden Ratio. The ratio of the height of a person to the height of his navel is the Golden Ratio 1.618.
The ratio of the combined length of the hand and forearm to the length of the hand is 1.618. The ratio of the length of hand plus forearm to the upper arm is 1.618. Similarly the ratio of the length of foot plus shin to the length of foot is 1.618.
An ideal human face consists of an abundance of Golden Ratio. A beautiful face will perfectly fit into a Golden Rectangle. Some of the Golden Ratios in the human face are:
- Length of face to Width of face;
- Length of face to the distance between the tip of the jaws and where eyebrows meet;
- Length of mouth to width of nose;
- Distance between the lips and the point where eyebrows meet to the Length of nose.
Our fingers have 3 sections (with the exception of thumbs). The ratio of the total length of a finger to the length of first two sections is in Golden Ratio.
The human lungs are divided asymmetrically into two bronchi, one long and one short. It is followed by asymmetrical subdivision too and in all cases the proportions are in the Golden Ratio.
DNA molecule of humans is based on the Golden Ratio. It consists of two entwined perpendicular helixes and has a curve length of 34 angstroms and a width of 21 angstroms for each full cycle of its double spiral helix. 34 and 21 are Fibonacci numbers and their ratio is the Golden Ratio.
Cochlea is a bony structure inside human ear that helps to transmit sound vibrations. It is constructed in spiral shape and follows the Golden Ratio.
Conclusion
Why does nature fascinate us with so many mathematical patterns that reflect the Fibonacci sequence and Golden Ratio? Can it be coincidence? May be; in some cases. But, it is definitely the law of the nature. When you ask your teacher why you should learn Mathematics, the teacher will tell you that you will need it for calculation and will be useful in your future. But, in your schooldays, nobody might have convinced you about the ‘omnipresence’ of Mathematics in nature. However, as you grow and climb on the top of the world, investigating and conquering the unknown ‘x’ , and always keeping the ‘why’ in the corner of your lips, you have become conscious of the beauty of mathematics in nature, in every moment of your breath. But, plants, like everything else in nature, do not know that they are using Fibonacci numbers or Golden Ratio in their growth pattern. Plants are trying to survive against all physical constraints and continuing their life cycles within the realms of their botanical universe, with a natural rhythm; but, without being aware of the Mathematics behind them……… And, of course, plants do not know Mathematics!!
Image Source: Wikimedia Commons
Like it on Facebook, Tweet it or share this article on other bookmarking websites.